CHAP 2. 확률
✖️ 표본공간과 사상
🔹 표본공간 (Sample Space, S)
통계적 실험 시행에서 나올 수 있는 모든 가능한 결과들의 집합
• 이산 표본공간 (Discrete Sample Space)
- • 유한: 가능한 결과가 유한한 경우 (예: 동전 던지기 {앞면, 뒷면})
- • 무한: 가능한 결과가 무한한 경우 (예: 자연수 집합)
• 연속 표본공간 (Continuous Sample Space)
- • 결과가 연속적인 값으로 표현될 수 있는 경우 (예: 0과 1 사이의 실수 값)
🔹 사상, 사건 (Event, A, B, …)
표본공간의 부분집합을 의미
• 기본사건 (Elementary Event): 하나의 원소로 이루어진 사건
예) 주사위를 던졌을 때 {3}이 나오는 사건
• 공사건 (Null Event, ∅): 일어나지 않는 사건
• 곱사건 (Intersection, ∩): 두 사건이 동시에 발생하는 사건
예) 주사위를 던졌을 때 짝수(2,4,6)이고 동시에 3 이하인 경우 → {2}
• 합사건 (Union, ∪): 두 사건 중 하나라도 발생하는 사건
예) 주사위를 던졌을 때 짝수 또는 3 이하인 경우 → {1,2,3,4,6}
• 여사건 (Complement, Aᶜ): 어떤 사건이 발생하지 않는 사건
예) A가 “주사위 눈이 짝수”일 때, Aᶜ는 “주사위 눈이 홀수”
• 배반사건 (Mutually Exclusive Event): 서로 동시에 발생할 수 없는 사건
예) 주사위를 던질 때 “짝수가 나올 사건”과 “홀수가 나올 사건”
✖️ 계수기법
계수기법은 사건의 개수를 효율적으로 계산하는 방법
🔹 1. Laplace의 확률
전체 가능한 경우 중 특정 사건이 발생할 경우의 수
P(A) = n(A) / n(S)
🔹 2. 곱법칙 (Multiplication Principle)
여러 개의 선택 과정에서 경우의 수를 곱하는 법칙입니다.
• 어떤 실험이 k개의 단계로 이루어져 있고,
• 첫 번째 단계에서 n1가지 방법
• 두 번째 단계에서 n2가지 방법
• …
• k번째 단계에서 nk가지 방법
이 있을 때, 전체 경우의 수는: n1 * n2 * .... nk
🔹 3. 순열 (Permutation, 순서 고려)
서로 다른 n개 중에서 r개를 선택하여 나열하는 방법의 수
즉, 순서가 중요한 경우의 수를 계산할 때 사용
nPr = n! / (n-r)!
🔹 4. 조합 (Combination, 순서 무관)
서로 다른 n개 중에서 r개를 선택하는 방법의 수
즉, 순서를 고려하지 않는 경우의 수를 구할 때 사용
nCr = n! / (n-r)! * r!
✖️ 확률의 정의
🔹 Kolmogorov의 공리적 확률 (Axiomatic Probability)
확률은 실수 값 함수 P로 정의되며, 다음 세 가지 공리를 만족
1️⃣ 어떤 사건 A의 확률은 항상 0 이상
2️⃣ 표본공간 전체의 확률은 1
3️⃣ 서로 배반사건일 경우, 확률은 덧셈 법칙을 따른다
✖️ 확률의 성질

✖️ 조건부 확률 (Conditional Probability)
어떤 사건 A가 발생한 상태에서 B가 발생할 확률
단 P(A) > 0
P(B | A) = P(A ∩ B) / P(A) = n(A ∩ B) / n(A)
• P(B | A) : A가 발생했을 때 B가 발생할 확률
• P(A ∩ B) : A와 B가 동시에 발생할 확률
• P(A) : A가 발생할 확률 (단, P(A) > 0 이어야 함)
✖️ 연관성 분석 (Association Rules)
조건부 확률을 활용하여 데이터의 연관성을 분석하는 기법
• 지지도 (Support): A와 B가 동시에 발생한 비율
• 신뢰도 (Confidence): A가 발생했을 때 B도 발생할 확률 ( P(B|A) )
• 향상도 (Lift): B가 발생할 확률과 비교하여 A와 B의 연관성 평가
✖️ 확률의 곱법칙
두 사건 A, B가 동시에 일어날 확률을 구하는 방법
즉, A가 발생한 상태에서 B가 발생할 확률 또는 B가 발생한 상태에서 A가 발생할 확률을 이용하여
A와 B가 동시에 발생할 확률 P(A ∩ B) 를 구할 수 있음
🔹확률의 곱법칙 정의
두 사건 A ,B 가 있을 때, 동시에 발생할 확률은 다음과 같이 계산

또는
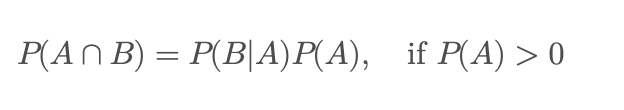
• : A와 B가 동시에 발생할 확률
• : B가 발생한 조건하에서 A가 발생할 확률
• : A가 발생한 조건하에서 B가 발생할 확률
• , : 각각 A와 B가 발생할 확률
즉, A와 B가 동시에 발생할 확률은 한 사건의 조건부 확률과 다른 사건의 확률을 곱하여 계산
✖️ 사건의 독립성 (Independence)
두 사건 A와 B가 서로 독립 (Independent) 이라면:
한 사건이 발생하는 것이 다른 사건의 확률에 영향을 주지 않는 경우
즉, A의 발생 여부가 B의 확률에 영향을 주지 않을 때, 두 사건은 독립

즉,
• B가 발생했을 때 A의 확률이 그대로 유지된다면, A와 B는 독립
• A가 발생했을 때 B의 확률이 그대로 유지된다면, A와 B는 독립
🔹 독립 사건의 확률 공식
두 사건이 서로 독립이라면, 다음 공식이 성립

즉, A와 B가 동시에 발생할 확률은 각 사건의 확률을 곱한 값과 같음
'🔢 수학 > 확률 및 통계학' 카테고리의 다른 글
| ✖️ 확률과 통계학 : CHAP 3. 확률분포 // 확률변수와 확률분포, 이산확률분포, 연속확률분포 (0) | 2025.03.26 |
|---|---|
| ✖️ 확률과 통계학 : CHAP 2. 확률 // 베이즈 정리 (0) | 2025.03.26 |
| ✖️ 확률과 통계학 : CHAP1. 기술통계 // 변동 통계량, 그룹화된 자료, 줄기 잎 그림, 상자 그림 (0) | 2025.03.19 |
| ✖️ 확률과 통계학 : CHAP1. 기술통계 // 용어, 방법론, 측정 척도, 도수분포표/도수그래프, 위치 통계량 (0) | 2025.03.16 |



