어제 눈도 많이 오고 노을도 예뻤다
필굿
✖️ 변동 통계량
변동 통계량은 데이터의 분포가 얼마나 퍼져 있는지를 측정하는 통계 지표
산포도
📌 (1) 범위 (Range)
가장 큰 값과 작은 값의 차이
• 극단값(이상치)에 민감함.
📌 (2) 분산 (Variance )
데이터 값들이 평균에서 얼마나 떨어져 있는지를 제곱하여 평균을 낸 값
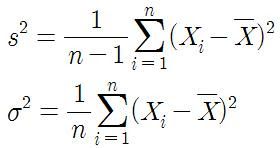
• 단위가 원래 데이터의 제곱 단위라 해석이 어려울 수 있음.
📌 (3) 표준편차 (Standard Deviation, )
분산의 제곱근을 취한 값
• 원래 데이터와 동일한 단위를 가짐.
• 데이터의 퍼짐 정도를 쉽게 해석 가능.
📌 (4) 사분위 범위 (Interquartile Range, IQR)
3사분위수(Q3) - 1사분위수(Q1)
• 극단값에 덜 민감하며 데이터의 중앙 부분 변동성을 측정하는 데 유용.
• Q1 (제1사분위수, 25%): 데이터의 하위 25%에 해당하는 값 (n+1)/4번째 값
• Q3 (제3사분위수, 75%): 데이터의 상위 75%에 해당하는 값 3(n+1)/4번째 값
✖️ 그룹화된 자료
연속형 데이터나 많은 데이터를 효율적으로 분석하기 위해 계급(interval) 으로 나눈 데이터 형태
mi = i 번째 계급구간의 중간점
fi = i번째 계급구간의 도수
n = 총관측수
📌 (1) 그룹화된 평균
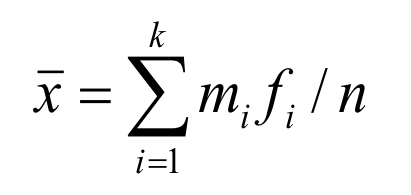
📌 (2) 그룹화된 분산
• 그룹화된 데이터의 변동성을 계산할 때 사용

✖️ 줄기 잎 그림
3️⃣ 줄기-잎 그림 (Stem-and-Leaf Plot)
줄기-잎 그림은 데이터를 정렬하면서 개별 값을 유지할 수 있는 시각화 방법
데이터 손실 없음!!!
하지만 데이터 개수가 많아지면 한눈에 확인이 어려움ㅠㅠ
📌 줄기-잎 그림의 구조
• 데이터의 앞자리(십의 자리 등) 는 “줄기(stem)”
• 데이터의 뒷자리(일의 자리 등) 는 “잎(leaf)”
예제
2 | 1 3 5
3 | 0 1 2 5
4 | 0 1 2 5 8✖️ 상자 그림
분포 모양, 분포 집중도, 범위 등을 한눈에
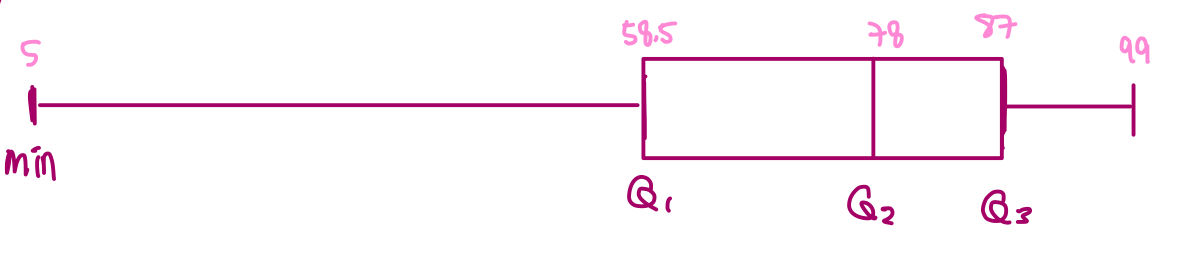
📌 상자 그림의 구성 요소
1. 최솟값 (Minimum): 이상치가 없는 경우 가장 작은 값
2. 제1사분위수 (Q1): 하위 25% 지점
3. 중앙값 (Q2, Median): 데이터의 중앙
4. 제3사분위수 (Q3): 상위 75% 지점
5. 최댓값 (Maximum): 이상치가 없는 경우 가장 큰 값
✖️ 이상점을 탐지하는 상자 그림
📌 상자 그림의 구성 요소
...
+ 6. 이상치 (Outlier): 이하 또는 이상의 값
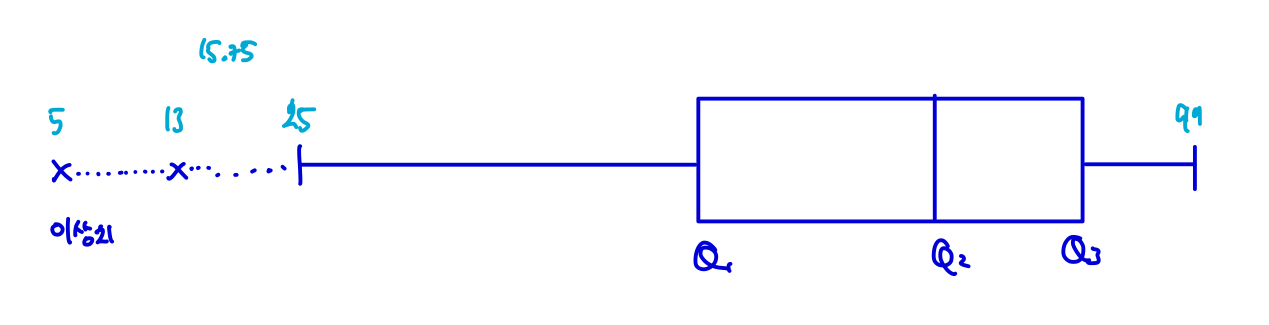
아래울타리 lower fence = Q1 - ( 1.5 * IQR )
윗울타리 upper fence = Q3 + ( 1.5 * IQR )
해당 울타리를 벗어나는 값은 이상치 처리
'🔢 수학 > 확률 및 통계학' 카테고리의 다른 글
| ✖️ 확률과 통계학 : CHAP 3. 확률분포 // 확률변수와 확률분포, 이산확률분포, 연속확률분포 (0) | 2025.03.26 |
|---|---|
| ✖️ 확률과 통계학 : CHAP 2. 확률 // 베이즈 정리 (0) | 2025.03.26 |
| ✖️ 확률과 통계학 : CHAP2. 확률 // 표본공간과 사상, 계수기법 , 확률의 정의, 성질, 조건부 확률, 연관성 분석 (0) | 2025.03.20 |
| ✖️ 확률과 통계학 : CHAP1. 기술통계 // 용어, 방법론, 측정 척도, 도수분포표/도수그래프, 위치 통계량 (0) | 2025.03.16 |



