🌳 이진 트리 🌳
각 노드의 자식 노드의 개수가 2 이하로 구성되어 있는 트리
(가장 많이 사용되는 형태)
🌳 종류
| 편향 이진 트리 | 노드들이 한쪽으로 편향된 이진 트리 | 탐색 속도가 저하되고 공간이 많이 낭비됨 |
| 포화 이진 트리 | 트리 높이가 모두 일정 / 리프 노드가 꽉 찬 이진 트리 | |
| 완전 이진 트리 | 마지막 레벨을 제외하고 완전하게 노드들이 채워진 / 마지막 레벨은 왼쪽부터 채워진 이진 트리 | 일반적인 형태 |
🌳 트리의 노드와 인덱스 간 상관관계
| 루트 노드 | 인덱스 = 1 | |
| 부모 노드 | 인덱스 = 현재인덱스 / 2 (몫) | 현재 노드가 루트 노드가 아닌 경우에 |
| 왼쪽 자식 노드 | 인덱스 = 현재인덱스 * 2 | 현재인덱스 * 2 가 전체노드 개수보다 작거나 같을 때 |
| 오른쪽 자식 노드 | 인덱스 = 현재인덱스 * 2 + 1 | 현재인덱스 * 2 + 1 가 전체노드 개수보다 작거나 같을 때 |
🥈 실버 1
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
⭐️ 순회 방법 ⭐️
🌟전위 순회 : 루트 -> 왼쪽 자식 -> 오른쪽 자식
🌟중위 순회 : 왼쪽 자식 -> 루트 -> 오른쪽 자식
🌟후위 순회 : 왼쪽 자식 -> 오른쪽 자식 -> 루트
(전중후 뜻은 루트(현재노드) 순서로 보면 됨)
🌟층별 순회 : 층별로 왼쪽 -> 오른쪽
예시
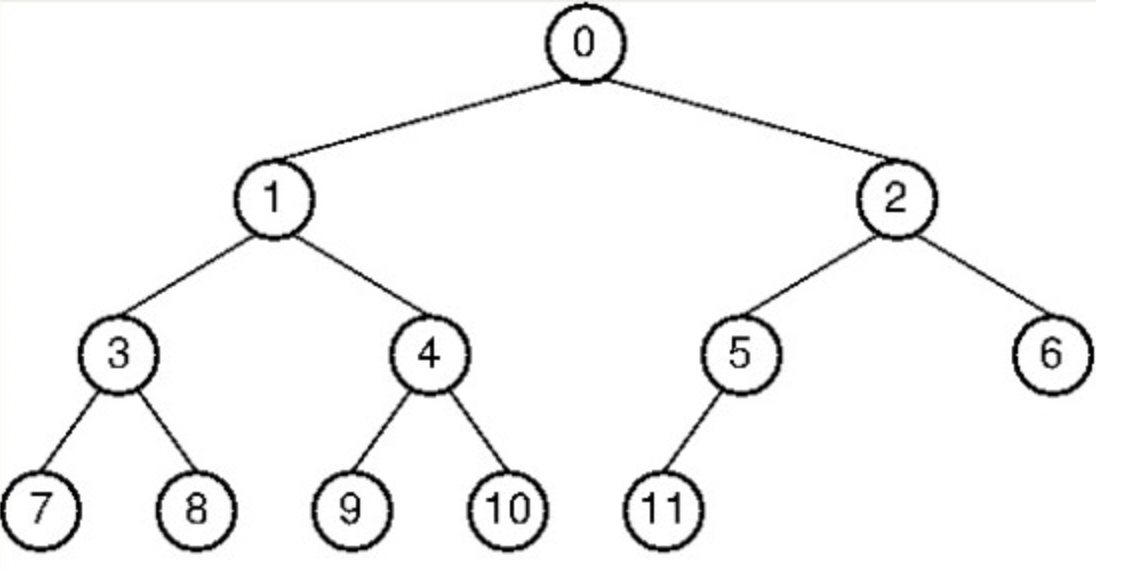
전위 순회 :
0 루트 -> 1 왼쪽 자식 (0루트트리)이자 루트 됨-> 왼쪽 3 (1루트트리)이자 루트 됨-> 왼쪽 7 (3루트트리)->오른쪽 8(3루트트리)->오른쪽 4(1루트트리)이자 루트 됨-> 왼쪽 9(4루트트리)->오른쪽 10(4루트트리)-> 오른쪽 2(0루트트리)이자 루트 -> 5(2루트트리)이자 루트->왼쪽 11 (5루트트리)->오른쪽 6
중위 순회 :
맨 왼쪽 시작 7 -> 부모 3 -> 오른쪽 8 (378서브트리 == 1의 왼쪽 자식 완성) -> 부모 1 -> (9410 서브트리, 1의 오른쪽 자식 할 차례)(전체 트리처럼 맨 왼쪽 시작) 왼쪽 9->부모 4-> 오른쪽 10 (루트가 1인 서브 트리 == 0의 왼쪽 자식 완성 )-> 부모 0 -> (0의 오른쪽 자식인 루트2서브트리 순회할 차례)(맨 왼쪽 시작) 11-> 부모 5-> 부모 2->오른쪽 6
후위 순회 : 맨 왼쪽 시작 7 -> 같은 층 오른쪽 8->부모 3 (378서브트리 == 1의 왼쪽 자식 완성) ->(4910서브트리 == 1의 오른쪽 자식 순회 시작) 9->10->4->1->11->5->6->2->0
그니까 서브 트리들로 잘라가면서 보면 됨
from sys import stdin
N = int(stdin.readline())
dic = {}
for _ in range(N):
root, l, r = stdin.readline().rsplit()
dic[root] = [l,r]
def fir(node): # 루트 왼쪽 오른쪽
if node == '.':
return
print(node, end ='') #루트
fir(dic[node][0]) #왼쪽
fir(dic[node][1]) #오른쪽
fir('A')
print()
def mid(node): # 왼쪽 루트 오른쪽
if node == '.':
return
mid(dic[node][0]) #왼쪽
print(node, end ='') #루트
mid(dic[node][1]) #오른쪽
mid('A')
print()
def last(node): # 왼쪽 오른쪽 루트
if node == '.':
return
last(dic[node][0]) #왼쪽
last(dic[node][1]) #오른쪽
print(node, end ='') #루트
last('A')'📊 Algorithm > Algorithm 주제별 정리' 카테고리의 다른 글
| 🧚♂️알고리즘🧚♂️ - 🌴 - 최소 공통 조상 (LCA 알고리즘) (0) | 2023.08.02 |
|---|---|
| 🧚♂️알고리즘🧚♂️ - 🌴 - 세그먼트 트리 (0) | 2023.07.31 |
| 🧚♂️알고리즘🧚♂️ - 🎄 - 트라이 (0) | 2023.07.18 |
| 🧚♂️알고리즘🧚♂️ - 트리🎄 (0) | 2023.07.18 |
| 🧚♂️알고리즘🧚♂️ - 그래프 - 최소신장트리 (0) | 2023.07.15 |



