..ㅇ
ㅓ려
ㅂ
가설의 역할과 구조
- 가설 h: 새로운 집의 크기 등을 입력받아 가격을 예측하는 함수.
- 단순한 선형 형태:여기서 x는 집 크기, \theta_0는 편향(bias), \theta_1은 기울기.
- 수학적으로는 편향이 포함되므로 “affine” 함수지만, 머신러닝에서는 종종 선형 함수라 부름.
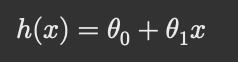
- 다중 특성 확장:h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2h_\theta(x) = \sum_{j=0}^n \theta_j x_j = \theta^T x


- 벡터 표현으로 정리됨.
- m: 학습 예제 수 (행 개수)
- n: 특성의 수 (bias 제외)
- x^{(i)}, y^{(i)}: i번째 학습 예제의 입력 특성 벡터와 타깃
- \theta: 학습할 파라미터 벡터 (\theta_0, \theta_1, \dots)
- h_\theta(x): 파라미터 \theta에 의해 정의되는 예측 함수(가설)
- x_0 = 1로 둠으로써 \theta_0를 상수항으로 포함시킴
학습 알고리즘 설계에서의 핵심 결정 요소
- 데이터 수집 (training set)
- 가설 공간의 정의 (어떤 형태의 h를 쓸지)
- 파라미터 표현 방식 (벡터화, 편향 처리 등)
- 목적: 주어진 데이터에 대해 “좋은” 예측을 하도록 \theta를 정하는 것
가설(hypothesis)의 일반화된 표현
- 단일 특성 x에 대한 예측은 보통이고, 여기서 \theta_0는 상수항(편향, bias), \theta_1은 기울기다.
- 수학적으로는 \theta_0가 들어가면 엄밀히 “affine” 함수지만 머신러닝에서는 관례적으로 선형 함수(linear function)라 부르는 경우가 많다.
- h(x) = \theta_0 + \theta_1 x
- 다중 특성이 있을 때 (예: 집 크기 x_1, 침실 수 x_2)이런 식으로 각 특성에 대응하는 계수를 더하는 선형 조합으로 표현한다.
- h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2
표기 간소화: x_0 = 1 도입과 벡터화


학습 알고리즘의 목적: 파라미터 \theta 선택

기호(Notation) 정리

차원 관계 정리
- 특성이 n개면, 편향을 포함시켜 입력 벡터 x와 파라미터 \theta는 각각 n+1 차원.x = \begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix},\quad \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix}, \quad h_\theta(x) = \theta^T x
- 예: n=2일 때
h_\theta(x)와 y를 가깝게 만들기
- 학습의 목적은 각 훈련 예제에 대해 예측 h_\theta(x^{(i)})가 실제 y^{(i)}와 “가까워지도록” \theta를 조정하는 것.
- 이 직관을 수식적으로 실현하려면 h_\theta(x^{(i)})와 y^{(i)}의 차이를 측정하는 기준이 필요하다. (다음 부분에서 비용 함수 J(\theta)로 정리됨)
- 즉, 전체 훈련셋 \{(x^{(i)}, y^{(i)})\}_{i=1}^m에 대해 예측 오차를 작게 하는 \theta를 찾는 문제로 귀결된다.
관점과 확장
- 표기상의 유연성: h(x) vs h_\theta(x) 구분은 “무엇이 변수인지”를 명확히 하려는 것이며, 이후 비용 함수나 최적화에서 \theta를 바꾸는 대상임을 드러낸다.
- 벡터화: 모든 m개의 예측을 한꺼번에 X\theta로 계산할 수 있도록 디자인 매트릭스 X를 구성하면 효율적이다.
- 확장: 특성을 늘리거나 변환(예: 다항식 항, 상호작용 항)해도 같은 \theta^T x 형태로 일관되게 다룰 수 있다.
목표: 파라미터 \theta를 선택해서 예측과 실제가 가까워지게 만들기
- 선형 회귀 알고리즘(ordinary least squares)은 예측 h_\theta(x)와 실제 타깃 y의 제곱 오차를 최소화하는 \theta를 찾는 것.
- 훈련 예제 m개에 대해 전체 오차를 합치면 비용 함수는:여기서 \frac{1}{2}는 미분할 때 2가 내려와 깔끔하게 하기 위한 관례적인 상수다.
- J(\theta) = \frac{1}{2} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2
왜 제곱 오차인가?
- 제곱 오차를 쓰는 것은 단순한 수학적 편의뿐 아니라 확률적 해석이 있다:
- 출력에 정규분포(Gaussian) 잡음을 가정할 때, 최대우도추정(MLE)을 하면 제곱 오차를 최소화하는 형태로 귀결된다.
- 다른 선택지들:
- 절대오차 |h_\theta(x) - y|: 라플라스(Laplace) 잡음 모델과 대응되고, 이상치에 덜 민감한 로버스트 회귀.
- 고차승(예: 4제곱): 이상치에 더 민감하고 에러 분포에 대한 다른 가정을 반영.
- 손실 함수 선택은 근본적으로 데이터의 노이즈 특성과 목적(robustness vs smoothness)에 따라 달라진다.
- 정의된 비용 J(\theta)를 최소화하기 위해 반복적 방법이 필요하다.
- 여기서 등장하는 첫 번째 일반적인 방법이 그래디언트 디센트(gradient descent).
- J(\theta)의 기울기를 따라 내려가며 \theta를 갱신해서 최소값을 찾는다.
- (다음 부분에서 구체적인 업데이트 식과 변형—batch, stochastic 등—이 소개될 예정)
Gradient Descent 직관
- 목적: 정의된 비용 함수 J(\theta)를 줄이기 위해 파라미터 \theta를 반복적으로 갱신.
- 비유: J(\theta)를 지형의 높이로 보면, 현재 위치(현재 \theta)에서 “가장 급하게 내려가는 방향”을 찾아 조금씩 내려가면서 최소값(낮은 지점)으로 이동하는 과정.
- 시작점: \theta는 보통 \mathbf{0} 벡터 or 무작위로 초기화. 선형 회귀에서는 로컬 미니마가 없어서 초기화 민감도가 크지 않음.
업데이트 규칙 (한 성분 기준)
- 비용 함수가일 때, \theta_j에 대한 편미분은
- \frac{\partial J}{\partial \theta_j} = \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}
- J(\theta)=\frac{1}{2}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2
- 한 스텝 갱신:여기서 \alpha는 학습률(learning rate).
- \theta_j := \theta_j - \alpha \cdot \frac{\partial J}{\partial \theta_j} = \theta_j - \alpha \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}
- “빼는 이유”: gradient는 증가하는 방향을 가리키므로 비용을 줄이려면 그 반대 방향으로, 즉 -\alpha \nabla J만큼 이동해야 한다.
전체 벡터화된 형태
- 디자인 매트릭스 X와 타깃 벡터 y를 쓰면 그래디언트는이고, 벡터화된 업데이트는(강의에서는 J에 \frac{1}{2}만 있고 \frac{1}{m}을 안 넣었기 때문에 위 식에서 1/m은 생략되어 있음. 평균을 취하는 형태로 정의하면 \frac{1}{m}X^T(X\theta - y)가 된다.)
- \theta := \theta - \alpha X^T (X\theta - y)
- \nabla_\theta J(\theta) = X^T (X\theta - y)
Batch vs Stochastic
- Batch Gradient Descent: 모든 m개의 훈련 샘플을 사용해 한 번에 그래디언트를 계산하고 업데이트. 정확하지만 데이터가 크면 비용이 큼.
- Stochastic Gradient Descent: 각 학습 예제 (x^{(i)}, y^{(i)})마다 그 하나만으로 업데이트. 궤적은 잡음이 섞여 진동하지만 평균적으로 글로벌 최소로 향함. 대규모 데이터에서 훨씬 빠른 진척.
학습률 선택
- \alpha가 너무 크면 overshoot(발산), 너무 작으면 느리게 수렴.
- 실전: 특성 스케일을 맞춘 뒤(예: [-1,1]이나 [0,1]) \alpha=0.01 같은 값으로 시작해 지수적 스케일(예: 0.001, 0.01, 0.1)로 여러 값을 시험해 본다.
- 보통 학습이 진행됨에 따라 \alpha를 천천히 줄여 진동 크기를 줄이는 스케줄링도 많이 사용됨.
로컬 미니마 관련
- 일반적인 비선형 문제와 달리, 선형 회귀의 비용 함수는 이차형(quadratic)이고 “큰 그릇” 모양이라 글로벌 최소만 존재한다. 따라서 초기화에 따라 다른 로컬 미니마에 빠질 걱정은 없음. (단, 정규화나 특성 다중공선성 등 수치적 문제는 별도 처리 필요)
요약된 단계
- \theta 초기화 (예: 0 벡터)
- 반복:
- 전체 데이터(Batch) 또는 개별 샘플(Stochastic)로 그래디언트 계산
- \theta := \theta - \alpha \cdot \text{gradient}
- 수렴 판단: 비용이 더 이상 의미 있게 줄어들지 않거나 변화가 미미할 때 종료
Gradient Descent 개요
- 목표: 비용 함수 J(\theta)를 줄이기 위해 파라미터 \theta를 반복적으로 갱신.
- 직관: J(\theta)를 산처럼 생각하면, 현재 위치에서 가장 가파르게 내려가는 방향(그래디언트의 반대 방향)으로 조금씩 걸어 내려가서 최저점(글로벌 최소)까지 도달하는 과정이다.
- 초기화: 보통 \theta = \mathbf{0}이나 무작위로 시작해도 되고, 선형 회귀에서는 로컬 미니마가 없기 때문에 초기값에 크게 민감하지 않다.
업데이트 규칙
- 각 파라미터 \theta_j는 다음처럼 갱신된다:여기서 \alpha는 학습률(learning rate), \frac{\partial J}{\partial \theta_j}는 해당 방향으로의 기울기(증가 방향)다.
- \theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j}
- 그래서 기울기를 빼는 이유는 비용을 줄이려면 증가 방향이 아니라 감소 방향으로 이동해야 하기 때문이다. 예: J(\theta)=\theta^2에서 \theta=1일 때 도함수(그래디언트)는 양수 2이므로 \theta := \theta - \alpha \cdot 2로 줄여야 J가 작아진다.
전체 벡터화된 표현 (Batch Gradient Descent)
- 디자인 매트릭스 X, 타깃 벡터 y를 쓰면 그래디언트는
- \nabla_\theta J(\theta) = X^T (X\theta - y)
- 벡터화된 업데이트:
- \theta := \theta - \alpha X^T (X\theta - y)
- 이 경우 한 iteration마다 **모든 m**개의 훈련 예제를 사용해서 한 번에 계산하므로 이를 batch gradient descent라 한다.
의사코드 (batch):
initialize theta (e.g., zeros)
while not converged:
gradient = X.T @ (X @ theta - y)
theta = theta - alpha * gradient
비용 함수의 구조와 수렴 안정성
- 선형 회귀의 비용 J(\theta)는 제곱합으로 구성된 **이차 함수(quadratic)**이므로 전체 공간에서 형태가 볼(bowl)처럼 생기고, 등고선은 타원(ellipse).
- 이 구조 때문에 로컬 최적해가 없고 유일한 글로벌 최소만 존재한다. 따라서 gradient descent는 적절한 학습률로 반복하면 결국 수렴한다.
- 등고선에서 가장 가파른 하강 방향은 항상 컨투어에 수직(orthogonal)이다.
시각적/직관적 설명
- 초기 가설(예: \theta = \mathbf{0})은 데이터를 설명 못 하는 수평선.
- 각 iteration마다 \theta가 조금씩 바뀌며 직선이 데이터에 더 잘 맞춰지고, 반복하면 점차 좋은 직선(예측)이 된다.
- 이 과정을 2차원/3차원 등고선 위에서 “한 걸음씩 내려가는” 움직임으로 시각화할 수 있다.
학습률 선택
- \alpha가 너무 크면 overshoot(최저점을 지나치며 발산)하고, 너무 작으면 느리게 수렴.
- 실전에서는 특성 스케일링(예: 각 특성을 [-1,1] 또는 [0,1]로 맞춘 뒤)하고, \alpha를 지수적 스케일(ex: 0.001, 0.01, 0.1, 0.2 등)로 여러 값을 시도해 가장 빠르게 J(\theta)를 줄이는 값을 찾는다.
- 비용이 증가하면 학습률이 너무 큰 신호다.
Batch Gradient Descent의 단점
- 한 걸음(update)을 위해 매번 전체 데이터 m개를 훑어야 하므로, 데이터셋이 아주 클 경우(수백만~수억 샘플) 계산 비용이 크고 느리다.
- 이런 이유로 실제 대규모 환경에서는 stochastic 또는 mini-batch 변형이 더 자주 쓰인다 (다음 강의/부분에서 다룸).
Batch Gradient Descent의 한계
- 한 번 파라미터를 업데이트하려면 m개의 모든 훈련 샘플을 훑어야 하기 때문에, 데이터셋이 아주 클 경우(수백만, 수천만, 수억 샘플) 매번 전체를 스캔하는 비용이 매우 크다.
- 예: m이 수십수백만이면 하나의 gradient step을 위해 수백만 예제를 읽고 합산해야 하고, 수렴하려면 수백수천 번 그 과정을 반복해야 하므로 전체 계산량이 터무니없이 커진다.
- 이로 인해 batch gradient descent는 대규모 데이터에선 실용성이 떨어진다 (디스크 I/O, 메모리 스캔 비용이 병목).
대안으로서의 Stochastic Gradient Descent 도입(도입부)
- 전체 데이터를 매번 쓰지 않고도 조금씩 파라미터를 갱신할 수 있는 방법으로 **Stochastic Gradient Descent(SGD)**가 제시된다.
- 핵심 아이디어(이어서 나올 내용의 예고): 전체 m개를 합산하는 대신, 각각의 개별 학습 예제 (x^{(i)}, y^{(i)})에 대해 하나씩 gradient를 계산하고 그때그때 \theta를 업데이트한다.
- 이로써 한 스텝당 계산이 훨씬 가벼워져 큰 데이터셋에서도 빠르게 진척을 볼 수 있다.
- 경로는 잡음이 섞여 흔들리지만 평균적으로 비용을 줄이는 방향으로 수렴하게 된다.
비교 (의사코드 대조)
- Batch:
gradient = sum over all i of (hθ(x[i]) - y[i]) * x[i]
θ = θ - α * gradient
- Stochastic (도입 개념):
for each training example i:
gradient_i = (hθ(x[i]) - y[i]) * x[i]
θ = θ - α * gradient_i
Stochastic Gradient Descent (SGD)
- 핵심 아이디어: 전체 m개의 예제를 한꺼번에 쓰지 않고, 하나의 훈련 예제 (x^{(i)}, y^{(i)})씩 순회하면서 그 하나에 대한 그래디언트를 계산해 즉시 \theta를 업데이트한다.
- \theta_j := \theta_j - \alpha (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}
- 경로 특성: 각 샘플별로 업데이트하므로 이동 경로에 잡음(noise)이 섞여 진동하면서 움직이지만, 장기적으로 평균적으로는 글로벌 최소 방향으로 수렴한다.
- 수렴 성질: 완전히 수렴하지 않고 계속 진동하지만, 큰 데이터셋에서는 매 스텝이 가볍기 때문에 빠르게 실용적인 좋은 \theta를 얻을 수 있다.
- 실전 팁: 학습률을 서서히 줄이는 스케줄을 쓰면(learning rate decay) 진동 폭이 줄어들어 “근사 수렴”이 더 안정적으로 된다.
- 정지 조건: 비용 J(\theta)를 시간에 따라 모니터링해서 더 이상 의미 있게 내려가지 않거나 변화가 작아졌다고 판단되면 멈춘다.
Batch vs Stochastic 비교 및 실용적 기준
- Batch Gradient Descent는 전체 데이터로 정확한 그래디언트를 계산하지만, 대규모 데이터에서는 한 스텝이 너무 느리다.
- SGD는 각 예제마다 빠른 업데이트를 해 실질적인 진전을 빨리 볼 수 있으며, 글로벌 최적을 정확히 찍지 않아도 “충분히 좋은” 파라미터를 얻는 경우가 많다.
- 데이터가 작으면 batch가 단순하고 안정적이므로 batch를 선호할 수 있고, 데이터가 크면 SGD나 mini-batch를 주로 사용한다.
Mini-batch 언급
- SGD의 중간 형태로, 한 번에 하나가 아니라 b개의 예제를 묶어서(예: 100개) 그 배치의 평균 그래디언트로 업데이트하는 mini-batch gradient descent가 있고, 실전에서 가장 널리 쓰이는 절충 방식이다.
Normal Equation (정규 방정식)으로 한 번에 최적해 구하기
- 목표: 반복적인 알고리즘 없이 닫힌 형태로 글로벌 최소 \theta를 직접 계산.
- 기본 표현:여기서 X는 디자인 매트릭스(각 행이 x^{(i)T}), y는 타깃 벡터.
- J(\theta) = \frac{1}{2}(X\theta - y)^T (X\theta - y)
- 미분 후 0으로 놓기:
- \nabla_\theta J(\theta) = X^T X \theta - X^T y = 0 \quad \Rightarrow \quad X^T X \theta = X^T y
- 해:이것이 normal equation. 한 스텝의 행렬 연산으로 글로벌 최소에 도달한다.
- \theta = (X^T X)^{-1} X^T y
행렬 미분과 트레이스 정리 (도입 배경)
- 벡터/행렬 함수의 미분을 깔끔하게 다루기 위해 다음 개념이 소개됨:
- 트레이스(trace): 정방행렬의 대각 성분 합. \text{trace}(A) = \sum_i A_{ii}, \text{trace}(A) = \text{trace}(A^T)
- 트레이스의 순환성: \text{trace}(AB) = \text{trace}(BA), \text{trace}(ABC) = \text{trace}(CAB)
- 행렬 함수 미분 예시: f(A) = \text{trace}(AB)일 때 \frac{\partial f}{\partial A} = B^T
- 이런 도구를 통해 J(\theta)를 벡터/행렬 형태로 전개하고, 그 도함수를 계산하여 정규 방정식을 유도할 수 있게 된다.
비가역성 및 실용적 대응
- X^T X가 비가역인 경우(특성들 사이에 선형 종속성이 있는 경우)에는 직접 역행렬을 취할 수 없으므로:
- **유사역행렬(pseudo-inverse)**을 쓰면 해를 얻을 수 있다.
- 근본 원인을 파악하려면 중복되거나 거의 종속적인 특성들을 찾아 제거하거나 재구성하는 것이 더 명확한 해결책이다.
'🤖 AI > AI' 카테고리의 다른 글
| 기계학습 오세은굣 중간/기말족보 (0) | 2025.10.26 |
|---|---|
| 📑 Stanford CS229 : Advice for applying Machine Learning 2 (0) | 2025.08.01 |
| 📑 Stanford CS229 : Advice for applying Machine Learning 1 (0) | 2025.05.23 |
| Stanford CS229 : Machine Learning 강의 (0) | 2025.04.23 |
| 🦿NLP / 감정분석(LSTM) 모델 훈련/평가 (0) | 2025.02.23 |

