🧚♂️ 백트래킹🧚♂️
현재 상태에서 가능한 모든 경로를 따라 들어가 탐색하던 중 원하는 값과 불일치하는 부분이 발생하면 이전 단계로 돌아가는 알고리즘
(DFS 연관)
실버3
15649번: N과 M (1)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
def backTracking():
if len(ans) == M: # 배열의 길이를 확인
print(" ".join(map(str, ans))) # 1 2 3 이런 상태로 출력하기 위해
return
for i in range(1, N+1): # 1 ~ N 까지
if i not in ans: # 중복 확인
ans.append(i) # 배열 추가
backTracking() # 재귀
ans.pop() # return으로 돌아오면 이게 실행됨. 1, 2, 3 일때 3을 없앰으로 전 단계로 돌아가는 것참고
https://veggie-garden.tistory.com/24
아아오끼~알지알지
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
퀸 : 상하좌우,대각선 공격할 수 있는 기물
N*N에 N개 놓으니까 각 줄에 한개씩 놓아야 함
from sys import stdin
N = int(stdin.readline())
result = 0
chess = []
def queen_check(i,j):
for q in chess:
if q[1] == j: # 일직선
return False
if abs(q[0]-i) == abs(q[1]-j): # 대각선
return False
return True
def backTracking(i): # 줄 i
global result
if i == N+1: # 공격불가판
result += 1
return
for j in range(1, N+1): # 1 ~ N 까지 요소 확인
if queen_check(i,j): # 퀸 놓을 수 있는지 확인
chess.append((i,j)) # 판에 추가
backTracking(i+1) # 재귀
chess.pop() # return으로 돌아오고 실행(전 단계로 돌아감)
backTracking(1)
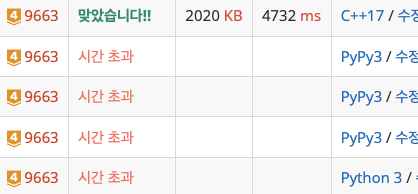
print(result)시간초과나잖아악
from sys import stdin
N = int(stdin.readline())
result = 0
chess = [0 for _ in range(N)]
def queen_check(a):
for i in range(a):
if chess[i] == chess[a]: # 일직선
return False
if abs(i-a) == abs(chess[i]-chess[a]): # 대각선
return False
return True
def backTracking(i): # 줄 i
global result
if i == N: # 공격불가판
result += 1
return
for j in range(N): # 1 ~ N 까지 요소 확인
chess[i] = j
if queen_check(i): # 퀸 놓을 수 있는지 확인
backTracking(i+1) # 재귀
backTracking(0)
print(result)이것도 시간초과나잖ㅏ!
#include <iostream>
#include <vector>
using namespace std;
int N;
int result = 0;
int chess[15];
bool queen_check(int a) {
for (int i = 0; i < a; i++) {
if (chess[i] == chess[a] || abs(i - a) == abs(chess[i] - chess[a])) {
return false;
}
}
return true;
}
void backTracking(int i) {
if (i == N) {
result += 1;
return;
}
for (int j = 0; j < N; j++) {
chess[i] = j;
if (queen_check(i)) {
backTracking(i + 1);
}
}
}
int main() {
cin >> N;
backTracking(0);
cout << result << endl;
return 0;
}그냥 c++로 그냐ㅐㅇ 넘어가야겟어
'📊 Algorithm > Algorithm 주제별 정리' 카테고리의 다른 글
| 🧚♂️알고리즘🧚♂️ - 조합/순열 2 (0) | 2023.09.06 |
|---|---|
| 🧚♂️알고리즘🧚♂️ - 동적 계획법(DP) 2 (0) | 2023.09.05 |
| 🧚♂️알고리즘🧚♂️ - 조합/순열 1 (0) | 2023.08.10 |
| 🧚♂️알고리즘🧚♂️ - 🌴 - 최소 공통 조상 (LCA 알고리즘) (0) | 2023.08.02 |
| 🧚♂️알고리즘🧚♂️ - 🌴 - 세그먼트 트리 (0) | 2023.07.31 |



