정렬 알고리즘에는 버블/선택/삽입/퀵/병합/기수 정렬이 있다
버블버블! 버블!
버블 정렬
두 인접한 데이터의 크기를 비교하여 정렬
시간 복잡도 O(n^2) (상대적으로 느린 편)
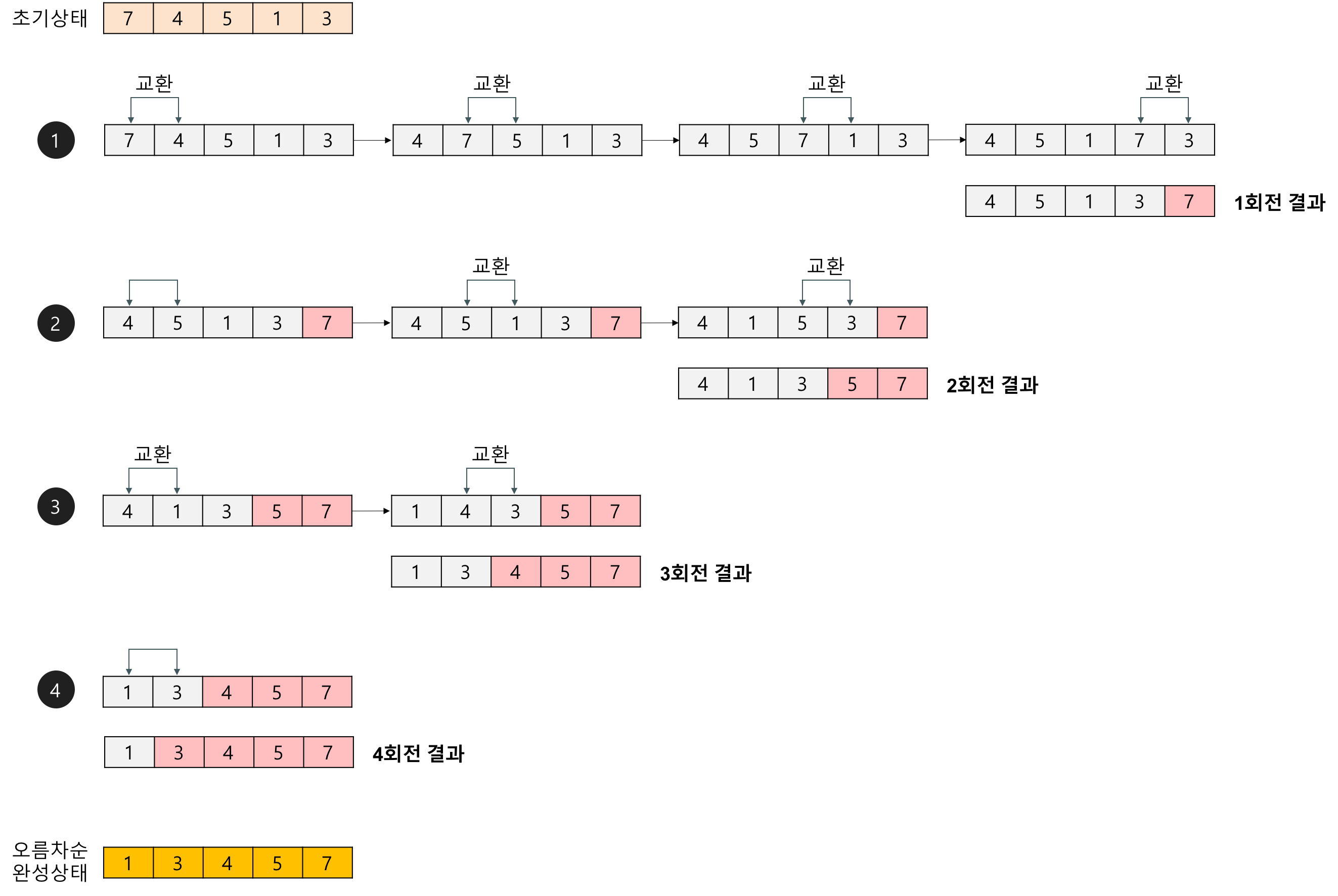
1) 비교 연산이 필요한 루프 범위를 설정한다
2) 인접한 데이터 값을 비교한다
3) swap 조건에 부합하면 swap 연산을 수행한다. (swap : 바꾸기)
4) 루프 범위가 끝날 때까지 2 - 3을 반복한다.
5) 정렬 영역을 설정한다. 다음 루프를 실행할 떄는 이 영역을 제외한다.
6) 비교 대상이 없을 때까지 1- 5를 반복한다.
만약 한 루프에서 swap이 한번도 일어나지 않았다면 정렬이 끝났단 뜻이므로 종료해도 됨
1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외되고,
2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외됨.
이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
그래서 데이터길이-1번 루프를 돌면 모두 정렬됨 (최대)
1.
2750번 브론즈 1
2750번: 수 정렬하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
슈도 코드
N(정렬할 수 개수)
A(수 저장 리스트 선언 및 입력 데이터 저장)
for 1을 0 ~ N-1만큼 반복:
for J를 0 ~ N-1-1만큼 반복:
현재 A 리스트의 값보다 1칸 오른쪽 리스트의 값이 더 작으면 두 수 바꾸기 # 스왑!
A 리스트 출력
from sys import stdin
N = int(stdin.readline())
A = [0]*N
for i in range(N):
A[i] = int(stdin.readline())
for i in range(N-1):
for i in range (N-1-i) :
if A[i] > A[j+1]: #swap~
temp = A[i]
A[i] = A[j+1]
A[i+1] = temp
for i in range(N) :
print(A[i])+
sort() 쓰면 바로 되긴 한다.
예전에 풀었던 코드 보니까 변수명까지 전부 똑같네..
from sys import stdin
N = int(stdin.readline())
Nlist = []
for i in range(N):
M = int(stdin.readline())
Nlist[i] = M
Nlist.sort()
for i in range(N):
print(Nlist[i])2.
1377번 골드 2
1377번: 버블 소트
첫째 줄에 N이 주어진다. N은 500,000보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에 A[1]부터 A[N]까지 하나씩 주어진다. A에 들어있는 수는 1,000,000보다 작거나 같은 자연수 또는 0이다.
www.acmicpc.net
- 버블 정렬의 swap이 한 번도 일어나지 않은 루프의 값을 찾아내는 문제 -> 즉 정렬이 완료된 지점이 언제인가?
- 버블 정렬로 풀면 시간복잡도 초과함 -> 데이터의 정렬 전 인덱스값과 정렬 후 인덱스값을 비교해 가장 왼쪽으로 많이 이동한 값을 찾으면 된다.
- 좌측으로 자리를 이동하는 경우는 i for문 내부에서 1번만 가능하기 때문!
슈도 코드
N(데이터 개수)
A(데이터 리스트, 단 클래스를 데이터로 담는 리스트)
for N만큼 반복:
A 리스트 저장
A 리스트 정렬
for N만큼 반복:
A[1]의 정렬 전 index - 정렬 후 index 계산의 최댓값을 찾아 저장
최댓값 + 1을 정답으로 출력
from sys import stdin
N = int(stdin.readline())
Nlist = []
for i in range(N):
Nlist.append((int(stdin.readline()), i))
Max = 0
sorted_Nlist = sorted(Nlist) # 정렬 기준을 고려하여 데이터, index 순서로 저장
for i in range (N) :
if Max < sorted_Nlist[i][1] - i: # 정렬 전 index - 정렬 후 index 계산의 최댓값 저장
Max = sorted_Nlist[i][1] - i
print (Max + 1)'📊 Algorithm > Algorithm 주제별 정리' 카테고리의 다른 글
| 🧚♂️알고리즘🧚♂️ - 정렬 - 삽입 정렬 (0) | 2023.01.16 |
|---|---|
| 🧚♂️알고리즘🧚♂️ - 정렬- 선택 정렬 (0) | 2023.01.10 |
| 🧚♂️알고리즘🧚♂️ - 자료구조 - 투 포인터 / 슬라이딩 윈도우 (0) | 2022.12.25 |
| 🧚♂️알고리즘🧚♂️ - 자료구조 - 스택.큐.덱 (0) | 2022.11.16 |
| 🧚♂️알고리즘🧚♂️ - 그리디 - 그리디 (2) | 2022.11.07 |



